Manifold
Manifolds (or differential manifolds) are one of the most fundamental concepts in mathematics and physics. A primitive definition of a manifold corresponds to a space that maybe curved and have a complicated topology, but in local regions looks just like \( \textbf{R}^n \). In other word, a manifold is a space consisting of patches that look locally like \( \textbf{R}^n \), and are smoothly sewn together. A manifold can also be defined as a set that has the local differential structure of \( \textbf{R}^n \) but not necessarily its global properties. However, a precise formulation of the concept of a manifold requires some preliminary definitions.
- Open ball
An open ball of radius \( r \) is the set of all points \( x \) in \( \textbf{R}^n \) such that \( |x-y| < r \) for some fixed \( y\in \textbf{R}^n \) and \( r\in \textbf{R} \), where \[ |x-y|=\left [\sum^n_{\mu=1} (x^\mu-y^\mu)^2\right]^{1/2}. \]
- Open set
An open set in \( \textbf{R}^n \) is any set which can be expressed as a union of open ball. This notion of open set makes \( \textbf{R}^n \) a topological space.
- Chart
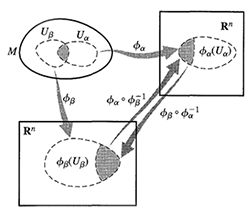
A chart or coordinate system consists of a subset \( U \) of a set \( M \) along with a bijective map \( \phi:U\longrightarrow \textbf{R}^n \), such that the image \( \phi(U) \) is open in \( \textbf{R}^n \).
- Atlas
A \( C^\infty \) atlas is a family of charts \( \{(U_\alpha,\phi_\alpha)\} \) which satisfies two following conditions:
1- The \( U_\alpha \) cover \( M \), \( i.e. \) \( \bigcup_\alpha U_\alpha =M. \)
2- If \( U_\alpha \bigcap U_\beta \) is non-empty, then the map \( \phi_\alpha \circ \phi_\beta^{-1}:\phi_\beta(U_\alpha \bigcap U_\beta)\longrightarrow \phi_\alpha(U_\alpha \bigcap U_\beta) \) is a \( C^\infty \) map of an open subset of \( \textbf{R}^n \) to an open subset of \( \textbf{R}^n \) (see figure 1).
- Manifold
A \( C^\infty \) n-dimensional manifold is a set \( M \) together with a \( C^\infty \) atlas \( \{(U_\alpha,\phi_\alpha)\} \) so that the above conditions are satisfied.